UQ-based metrics for chemical sustainability

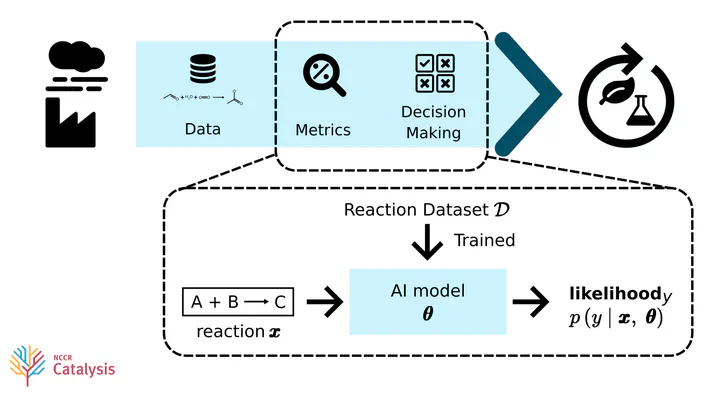
What if we could systematically quantify how sustainable a reaction is?

In this project (my master’s thesis at EPFL) I explored how useful it would be if we quantified sustainability as how likely it is that a reaction is sustainable. This likelihood would then be computed by employing uncertainty quantification (UQ) on some AI model’s prediction.

The main contribution of the project is an extensible toolkit with sustainability metrics based on AI model predictions.

In this page I collect some of my thoughts derived from this project.

You can read the full report here.

Table of Contents

AI-metric definition

Let’s say a chemical reaction can be one of $\mathcal{C}$ classes, for ex., according to its type: “carboxylic acid to acid chloride”, “translocase-catalyzed”, etc.

Some of these classes are sustainable, $\mathcal{C}_\text{sust}$ , some are not, $\mathcal{C}_\text{non-sust}$ , and we may have an unrecognized class, $\mathcal{C}_\text{unrec}=\{y_\text{unrec}\}$ .

Click to view the reaction type distribution

We can then quantify how likely we expect some reaction $\pmb{x}$ to be of some class $y\in\mathcal{C}$ :

$$ \text{AI-metric}_y := \mathbb{E}_{p(\pmb{\theta}\vert\mathcal{D})}\left[p(y\vert\pmb{x}, \pmb{\theta})\right]\cdot\text{confidence}(\pmb{x}, y) \quad \in [0,1]$$

Where $\pmb{\theta}$ are the parameters of our AI model after training it on some dataset $\mathcal{D}$ .

Note how we are scaling by how confident we are that this expected likelihood is correct. In our case,

$$\text{confidence}(\pmb{x}, y) := 1 - 2\cdot\text{stddev}_{p(\pmb{\theta}\vert\mathcal{D})}\big(p(y\vert\pmb{x}, \pmb{\theta})\big)$$

Which is always in $[0,1]$ since probabilities cannot deviate more than $1/2$ .

But, how do we score how likely our $\pmb{x}$ is of any class in $\mathcal{C}_\text{sust}$ ?

We simply take the maximum over $\mathcal{C}_\text{sust}$ :

$$\text{AI-metric} := \max_{y\in\mathcal{C}_\text{sust}} \text{AI-metric}_y \quad \in [0, 1] $$

Why not sum over$\mathcal{C}_\text{sust}$ ?

Formally, we are asking $p(\cup_{\mathcal{C}_\text{sust}}y\vert \pmb{x},\mathcal{D})$ , which is: $$ \max_{y\in\mathcal{C}_\text{sust}} p(y\vert\pmb{x},\mathcal{D}) \leq p(\cup_{\mathcal{C}_\text{sust}}y\vert \pmb{x},\mathcal{D}) \leq \sum_{y\in\mathcal{C}_\text{sust}} p(y\vert\pmb{x},\mathcal{D}) $$ Since we are estimating our metric (see next section) and since some $\pmb{x}$ may be of multiple classes, if we sum probabilities we would be overestimating the true value and also our score may end up above 1.
It is also crucial that in our case our AI model is single-label, so it is designed to only predict the highest probability class.

Modelling uncertainty

Without getting too philosophical, we want to believe that for sure there is some underlying true classification set for an input $\pmb{x}$ , $\mathcal{C}_\text{true} \subseteq \mathcal{C}$ , so:

$$ p(y\vert\pmb{x}) = \begin{cases}1 & \text{if }y\in\mathcal{C}_\text{true} \\ 0 & \text{o.w.}\end{cases} $$

Note that (by our philosophy) $p(y\vert\pmb{x})$ is equivalent to $p(y\vert\pmb{x},\mathcal{D}_\text{all})$ where $\mathcal{D}_\text{all}$ is all the knowledge of the universe (quite some information!).

Of course, in reality at best we know:

$$p(y\vert\pmb{x},\mathcal{D}) = \mathbb{E}_{p(\pmb{\theta}\vert\mathcal{D})}\left[ p(y\vert\pmb{x},\pmb{\theta}) \right]$$

For our observed training set $\mathcal{D}$ .

This means that we are in the presence of two sources of uncertainty¹:

1. Epistemic $\pmb{\theta}$ : due to the limited expresiveness of our model and its optimization procedure.
2. Aleatoric $\mathcal{D}$ : due to noise in our training set (some entries aren’t reactions or have a wrong label).

Quantifying AI-metrics

We use efficient uncertainty quantification (UQ) techniques to estimate our AI-metric according to the two sources of uncertainty²:

1. Monte Carlo Dropout (MCDropout) for epistemic uncertainty $\pmb{\theta}$ : We leave our Drouput layers on during inference, so for each forward pass on the same $\pmb{x}$ we are effectively sampling different submodels from an ensemble.

2. Test-time data augmentation for aleatoric uncertainty $\mathcal{D}$ : We augment $\pmb{x}$ during inference.

We then have $N\times M$ likelihoods $p(y\vert\pmb{x}^{(i)}, \pmb{\theta}^{(j)})$ where we sampled our input $\pmb{x}^{(1)},\dots,\pmb{x}^{(N)}$ and our model $\pmb{\theta}^{(1)},\dots,\pmb{\theta}^{(M)}$ . Our AI-metric then simply uses the average and stddev of these values to compute its score.

For example,

Validating AI-metrics

How useful is this metric definition? Is it really able to differentiate reactions $\pmb{x}$ in $\mathcal{C}_\text{sust}$ from those in $\mathcal{C}_\text{non-sust}$ ?

To answer this, I looked at two opposite scores:

Sustainability score: $\text{AI-metric} := \max_{y\in\mathcal{C}_\text{sust}} \text{AI-metric}_y $

Non-sustainability score: $\overline{\text{AI-metric}} := \max_{y\in\mathcal{C}_\text{non-sust}} \text{AI-metric}_y $

In particular, I quantify how likely it is that a reaction is enzymatic, since these types of reactions are a classical example of sustainable reactions.

First, I fine-tuned BERT on a training set of reactions in the SMILES text-based format, achiving an overall validation accuracy of 93.95% and macro F1 score of 0.901 when predicting the reaction type.

Then, we can compute $\text{AI-metric}$ and $\overline{\text{AI-metric}}$ using this BERT model for all reactions in the validation set and plot the results:

Clearly, enzymatic reactions cluster in blue separately from non-enzymatic ones in red.

Around here, our validation discussion of the AI-metric ends, but it would be interesting to study more in depth its applicability, in particular we could carefully design a dataset by artificially introducing aleatoric uncertainty and study how our AI-metric scores change as we increase data noise and as we underfit/overfit our model.

Don’t pay attention to the attention …

Of what use is a probabilistic metric if we cannot interpret the results? It’d be more appropriate if our toolkit of metrics also contained AI interpretability tools.

This is specially important since we may have high confidence in a wrong prediction. For example:

Our BERT model classifies the reaction as class EC.5, which means that is uses an isomerase enzyme. In reality the reaction is not enzymatic, it is of type 9.3.1 ("carboxylic acid to acid chloride"), and the AI-metric scores it as ~51% likely and confidently to be enzymatic. By our plot from the previous section, we’d simply look at this score and blindly accept it as enzymatic.

So what is going on?

We may want to look at what BERT is doing. In particular its attention scores:

Note how attention indicates that the model attributes attention to the OH and Cl exchange, which is precisely the rule for type 9.3.1. But the model of course does not predict the reaction as that type! What happens is that token embeddings at the last layer do not represent the corresponding token individually, but rather a global property in the text, so attention does not tell us the casual relationship learned between the input atomic structures and the output.

In fact, we should not look into attention attribution, but importance attribution, i.e. how each input affected the output.

With the Captum Python package we can see this importance attribution through the so-called method of Integrated Gradients³:

So now we see that OH and Cl exchange did not cause the model to predict the reaction type as EC.5, but some other structure.

Putting it all together

To summarize, this toolkit of AI-metrics is useful to automatically select reactions which are likely to be sustainable, but the resulting reactions should always be checked by a chemist expert to make sure that they are indeed sustainable.

We basically want to introduce a framework with sustainability metrics during the design cycle of molecule discovery, where our expert is still exploring which reactions may be feasible. This could, in principle, accelerate sustainable decision-making in chemistry.

A particular use-case for our toolkit is the multistep retrosynthesis task, where we want to find a path of reactions that can generate a target molecule from some starting molecules.

We simply generate many possible reaction paths for some target molecule using AiZynthFinder and Monte-Carlo tree search (MCTS)⁴.

Then, we select the best reaction path according to a weighted sum of our sustainability metrics and an estimation of the monetary cost to carry out the reactions.

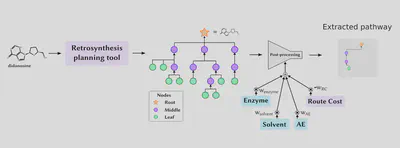
In this way, the expert can tune trade-offs between sustainability aspects by simply weighting the metrics.

We can do a quick ablation study and see how increasing the input weights on our enzyme AI-metric increases the enzyme AI-metric score, but also the route cost, so there is a trade-off between the two which can be tuned with the weights:

This is the end of this little blog, but you can find more details in the report.